Actual function of coils and capacitors

The electrical circuits that make up MCU interface are mainly DC circuits, so they are relatively simple, obeying Ohm's law with resistance as the load. However, when it comes to AC circuits, the story is different. This is because the coils and capacitors used in the circuits have a characteristic called impedance, which is the resistance value in a DC circuit that changes depending on the frequency of the flowing electrical signal, causing the phase of the signal voltage and current to shift.
Let me verify physically why the voltage phase shifts with respect to the current in an inductor and a capacitor, instead of relying only on mathematical formulas.
Coil:

A coil has the property of generating a current or magnetic field in a direction that interrupts the flowing current when it changes with time (back EMF opposite to the current is generated). This action makes the coil stabilize the current. In DC, the current flow is momentarily blocked, but once it settles, the coil becomes a mere conductor. In alternating current, it always acts like a resistance.


This effect is called inductive reactance XL (=ωL), which increases in proportion to inductance L and frequency ω (=2πf). Due to this property, in the case of an inductor, the current lags behind the phase of the voltage, which means that the phase of the voltage advances with respect to the phase of the current.
Capacitor:

Capacitors have the property that when a voltage is applied, the charge Q accumulates and charges, and when connected to a load with a lower potential than itself, it discharges(the current is at its maximum when a voltage is applied to an empty capacitor, whereas the voltage is at its minimum when empty and maximum when the charge is complete). The charge Q has the characteristic Q(t)=CV(t), which is proportional to the voltage V across the capacitance C. The current i(t) is the time variation of the charge Q(t) i=dQ/dt=Cdv/dt.
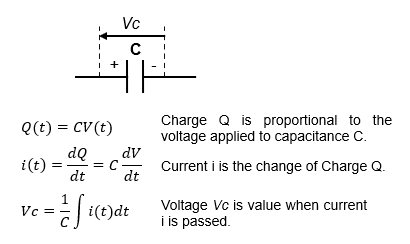

This action allows the capacitor to absorb voltage fluctuations, i.e., stabilize the voltage, and in the case of direct current, the capacitor is momentarily charged, but no further current is passed through it, only alternating current that repeatedly charges and discharges.

A capacitor always acts like a resistance in AC and is called a capacitive reactance XC (=1/ωC ), which is the opposite of a coil and decreases inversely proportional to the capacitance C and frequency. Due to this property, in the case of a capacitor, the current advances with respect to the phase of the voltage, i.e., the phase of the current is delayed with respect to the phase of the voltage.

The phase shift action is not that difficult to understand considering the properties of coils and capacitors learned in junior high school science class, but there are many explanations using only mathematical formulas, and if you think you understand only those formulas, you may lose sight of what is essential. If you are an engineer who handles things rather than a theorist, I recommend that you review the physical effects of coils and capacitors and reorganize your knowledge, even if you have only used mathematical formulas to understand them.